Einleitung
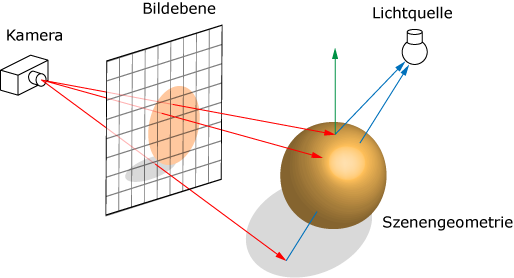
Raytracing ist eine Methode um realistische aussehende Bilder zu erzeugen, indem man den Transport des Lichtes nachahmt. Dies wird mit Hilfe von Strahlen (Rays) erreicht, die man mit der Geometrie der vorliegenden Szene schneidet. Dabei ermittelt man den von der Kamera aus nächstliegenden Schnittpunkt. Dazu wird für jeden Pixel der Bildfläche ein Strahl erzeugt. Ein naiver Algorithmus iteriert pro Strahl über alle Dreiecke der Geometrie, um den nächstliegenden Schnittpunkt für einen bestimmten Strahl zu ermitteln. Diese Methode (Brute-Force) ist vergleichsweise langsam. Mit Hilfe einer Beschleunigungsstruktur, kann die Schnittberechnung beschleunigt werden. Diese unterteilt die Geometrie räumlich und strukturiert die entstehenden Teilbereiche hierarchisch in einer Baumstruktur. Dabei verringert sich die Suche nach dem nächstliegenden Schnittpunkt im besten Fall von O(n) auf O(log n). Dennoch benötigt der Bau dieser Datenstruktur Zeit und zusätzlichen Speicher. Es gibt verschiedene Arten von Beschleunigungsstrukturen, welche sich in der Aufbauzeit, dem Speicherbedarf und der Renderzeit unterscheiden.
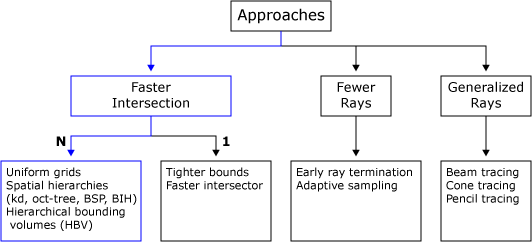
Beschleunigungsstruktur
Mithilfe von Beschleunigungsstrukturen ist es möglich die Anzahl der nötigen Schnitte mit der Geometrie im Vergleich zu einer Brute-Force-Methode drastisch zu reduzieren. Dazu wird die Geometrie so aufgeteilt, dass nicht geschnittener Raum garnicht erst betrachtet wird (Space Partitioning). Eine einfache Methode ist die Einteilung der Szene in ein einheitliches Gitter (Uniform Grid). Die Geometrie wird anhand des Gitters aufgeteilt, dadurch referenziert jede Zelle des Gitters die darin liegende Geometrie der Szene. Diese kann auch leer sein. Während dem Rendern schneidet man erst mit den Zellen des Gitters und danach mit der dahinter liegenden Gemoterie.
Eine andere Variante, die auch in diesem Projekt Anwendung fand, ist die Verwendung von Baumstrukturen (Spatial Hierachies). Dabei wird die Geometrie in einem Baum so sortiert, dass der Strahl später nur einen Pfad im Baum abarbeiten muss um zum nächesten Schnittpunkt zu kommen. Die Knotenpunkte des Baumes bestehen dabei meist aus kostengünstig zu schneidenden Primitiven (Planes, Cubes, Spheres). Im besten Fall kann die komplette Geometrie eines der Kinder verworfen werden, sollte ein Knoten nicht geschnitten werden. Die Laufzeit wäre dann n*log(n) wobei n die Anzahl der Dreiecke darstellt.
In der Arbeit wurden die folgenden drei Strukturen auf ihre Vor- und Nachteile untersucht:
- BVH
- k-d Baum
- BIH
Zur Wahl der Splitting-Plane
Für die Konstruktion einer räumlichen Beschleunigungsstruktur benötigt man eine Ebene an der die Geometrie der Szene geteilt wird. Das Volumen welches geteilt wird, ist durch die Bounding Box der Sezene gegeben. Die Ebene/Splittinplane, welche die Szene unterteilt, ist meist achsenparallel. Es gibt verschiedene Methoden zur bestimmung der Splitting-Plane, in diesem Projekt wurden die folgenden Heuristiken implementiert.
Median-Cut: Beim Median Cut wird die Splitting-Plane so gewählt, dass sie den Raum entlang einer Achse in zwei gleichgroße Volumen teilt. Es ist die trivialste Methode Geometrie aufzuteilen und resultiert in sehr schnellen Bauzeiten von Bechleunigungstrukturen. Die Aufteilung nimmt aber keine Rücksicht auf die Verteilung der Dreiecke im Raum und verursacht selten gute Ergebnisse in den Renderzeiten, da zum Beispiel sehr große überschneidungen beim BVH oder leerer Raum beim BIH nicht beachtet wird.
Surface Area Heuristic: Bei der Surface Area Heuristic (SAH) kann durch die Anwendung einer Funktion die Wahl der Splitting-Plane optimiert werden. Die Funtkion berechnet die Traversierungskosten für einen Split mit einer definierten Canidateplane. Die Canidateplane wird dabei an alle Vertices einer Szene angelegt (Exact SAH). Der Aufwand kann dabei sehr hoch sein, da für eine exakte Bestimmung sämtliche Vertices betrachtet werden müssen. Um die Berechnung zu beschleunigen, wird der Raum diskretisiert (Binned SAH). Für eine optimierte Struktur sollen diese Kosten minimiert werden. Die Kosten sind niedriger je mehr Dreiecke ein geringes Volumen in einer Teilszene einnehmen, denn so ist die Wahrscheinlichkeit am geringsten, dass eine Teilszene geschnitten wird.

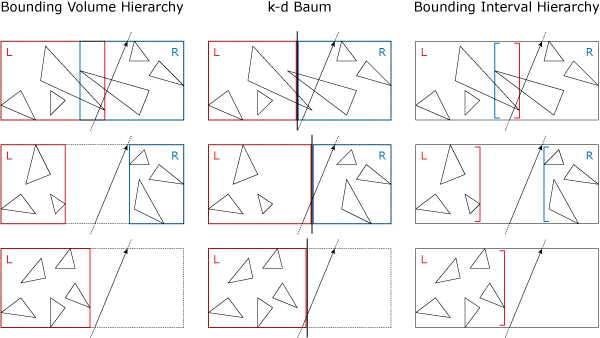
Bounding Volume Hierarchy (BVH)

Ein BVH ist ein binärer Baum bestehend aus Bounding Volumes (BV) in den Knoten und Geometrie (z.B. Dreiecke) in den Blättern. Ein Vaterknoten umschließt dabei alle seine Kinderknoten.
Konstruktion
Die Konstruktion ist sehr einfach, die einzige Variable beim Aufbau ist die Wahl der Splitting-Plane, also der Plane bei der die Dreiecke in das linke bzw. rechte Kind eingeteilt werden. Die Splitting-Plane wird mit Hilfe der Surface Area Heuristic (siehe SAH) gewählt, um ein mögliches Optimum bei geringen Bauzeiten zu erreichen. Optimal heißt hier, die Chance, dass ein Strahl ein Volumen schneidet soll möglichst gering sein. Das wird erreicht in dem BVs erzeugt werden die eine möglichst geringe Oberfläche besitzen. Wurde eine Spliting Plane gewählt wird ein Knoten aufgeteilt, das wird für alle entstehenden Knoten wiederholt, bis nur noch so viele Dreiecke in einem Knoten vorhanden sind, dass sich eine weitere unterteilung nicht lohnt.
Schnitt/Traversierung
Bei einem Schnitt von einem Strahl mit einer BVH wird als erstes der Rootknoten auf einen Stack gelegt. Der Algorithmus arbeitet dann den Stack ab. Dazu wird das oberste Element des Stacks genommen und geschnitten, erfolgt ein Schnitt werden die Kinder auf den Stack gelegt. Erfolgt ein Schnitt mit beiden Kindern müssen beide weiter mit dem Strahl geschnitten werden. Dazu werden beide Knoten auf einen Stack gelegt, das Kind welches weiter vom Kameraurpsrung entfernt ist wird zuerst abgelegt. Ist der Stack leer ist die Traversierung abgeschlossen. Befindet sich ein Schnittpunkt mit der Geometrie vor einem Schnittpunkt mit einem noch nicht bearbeiteten BV muss der zugehörige Knoten und dessen Kinder nicht mehr abgearbeitet werden.
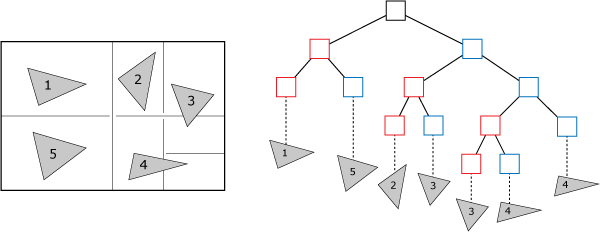
k-d Baum
Ein k-d Baum ist ein binärer Baum, der einen k-dimensionalen Raum hierarchisch mit Hilfe von Schnittebenen (Splitting-Planes) unterteilt.
Dabei speichern Blattknoten die Referenzen der Dreiecke, die sich im jeweilig repräsentierten Unterraum befinden und innere Knoten verwalten die Schnittebenen. Schneidet man nun die Struktur mit einem Strahl, so kann man den Baum traversieren und an Hand der Ebenen bestimmen, ob die von den entsprechenden Kindknoten aufgespannten Teilbäume traversiert werden müssen oder nicht. Dadurch kann die Anzahl der Dreiecksschnitte stark reduziert werden, allerdings müssen dafür Schnitte mit den Ebenen berechnet werden.
Ein k-d Baum lässt sich relativ einfach konstruieren, indem man den Raum und seine Unterräume mittels Median-Cut teilt. Allerdings ist diese Herangehensweise unter Umständen wenig effizient, da die Form der zu unterteilenden Struktur, beziehungsweise die Lage der Dreiecke zueinander, nicht berücksichtigt wird. So ist es in diesem Fall möglich, dass Knoten mit sehr vielen und Knoten mit sehr wenig Referenzen existieren (man stelle sich eine Szene vor, in der ein oder mehrere Anhäufungen von Dreiecken in Randbereich existieren). Beim Traversieren eines solchen Baumes kann es aus bestimmten Blickwinkeln zu starken Performanceeinbrüchen kommen.
Konstruktion
Um einen k-d Baum zu konstruieren muss man den Raum möglichst so aufteilen, dass die Kindknoten ein bestimmtes Volumen unterschreiten oder eine bestimmte Anzahl an Dreiecksreferenzen enthalten. Dazu nimmt man den obersten Knoten vom Stack und prüft, ob alle in ihm gespeicherten Dreiecke auch wirklich in seinem Volumen liegen (in wenigen Fällen kann es durch Bereichsvergleiche vorkommen, dass dies nicht der Fall ist). Nun versucht man die optimale Schnittebene zu finden oder das Volumen des Knotens zu verkleinern, indem man leeren Raum "abschneidet". Dabei wird ein leerer Kindknoten erzeugt und einer dessen Dreiecksliste mit der des aktuellen Knotens identisch ist. Dieser Vorgang wird als "Empty Space Clipping" bezeichnet. Auf diese Art unterteilt man den Raum nun so lange, bis jeder Kindknoten eine bestimmte Anzahl von Dreiecksreferenzen unterschreitet oder bis die über die SAH berechneten Traverierungskosten die Kosten des aktuellen Knotens nicht mehr unterschreiten (denn dann wäre es sinnlos, weiter zu unterteilen). Für den Aufbau des Baumes sind viele Daten notwendig, die bei der Traversierung irrelevant sind. Um die Datenstruktur möglichst klein zu halten und im Speicher zu ordnen ist es sinnvoll sie in eine kleinere, serialisierte Form zu überführen.
Das Finden von geeigneten Schnittebenen gestaltet sich oftmals als schwierig. Deswegen kam die SAH zur Anwendung.
Schnitt/Traversierung
Um herauszufinden, ob, beziehungsweise welche Dreiecke ein Strahl schneidet, traversiert man den k-d Baum. Ist der aktuelle Knoten ein innerer, so berechnet man den Schnittpunkt mit dem Strahl. Mit near wird der Schnittpunkt des Strahls mit der vorherigen Schnittebene bezeichnet, welcher dem Betrachter am nächsten ist. far bezeichnet den entsprechenden weiter entfernteren Schnittpunkt. Ist d größer far so schneidet der Strahl das vordere Kind, ist d kleiner near so wird das hintere Kind geschnitten. Liegt d zwischen near und far, so müssen beide Kinder traversiert werden. Hierbei wird das vordere zuerst untersucht und das hintere im Stack gespeichert. Trifft man auf einen Kindknoten so berechnet man für jedes Dreieck in seiner Liste den Schnittpunkt und fährt fort.

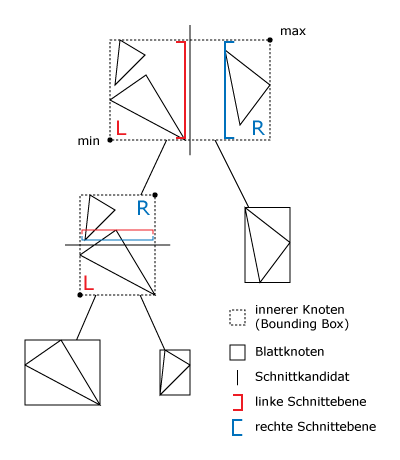
Bounding Interval Hierarchy (BIH)
Die Bounding Interval Hierarchy (BIH) ist eine hybride Beschleunigungsstruktur. Die Konstruktion der Struktur richtet sich nach der Aufteilung einer Objektliste, die Traversierung nutzt die Effizients räumlicher Aufteilung. Es ist möglich den Speicherbedarf im Voraus zu bestimmen.
Die Datenstruktur besteht aus zwei Arten von Knoten. Zum einen innere Knoten, welche zwei Referenzen auf deren Kindknoten enthalten, und zum anderen Blattknoten, welche eine Referenz auf den Anfang einer Dreiecksliste halten. Jeder innere Knoten besitzt zwei parallele Ebenen die zu einer der drei Koordinatenachsen orthogonal sind, dies ist die dominante Achse. Diese zwei Ebenen teilen den Knoten in einen rechten und einen linken Kindknoten auf. Die Kindknoten repräsentieren einen Unterraum des Vaterknoten, sind aber nicht zwangsläufig disjunkt (vgl. k-d Baum). Um die Kindknoten zu erzeugen wird die Bounding Box des Vaterknotens mit Hilfe der zwei Ebenen unterteilt. Dadurch entsteht ein linker und ein rechter Bereich die wiederum die Bounding Box der Kindknoten ergeben. Diese Bereiche können sich sowohl überlappen, ähnlich bei der BVH, sie können aber auch einen leeren Bereich zwischen den beiden Kindknoten erzeugen.
Ein innerer Knoten wird beschrieben durch die Position der beiden Ebenen und ein Index auf den ersten Kindknoten. Ein Blattknoten wird beschrieben durch einen Dreiecksindex und die Anzahl an Dreiecken, welche von diesem Knoten gehalten werden.
Konstruktion
Der Bau der BIH ist vergleichsweise simpel. Angenommen für den Wurzelknoten wurde ein optimaler Schnittkandidat mit Hilfe der SAH berechnet. Dieser Schnittkandidat teilt den Knoten orthogonal zu der gewählten Schnittachse. Als nächstes wird für jedes Dreieck innerhalb dieses Knotens bestimmt auf welcher Seite des Schnittkandidat es sich befindet. Danach werden die beiden Schnittebenen des Knotens bestimmt, indem entlang der Achse das Maximum und Minimum der linken und rechten Dreiecksmenge ermittelt wird. Daraufhin werden die Dreiecke im Speicher neusortiert, damit die Dreiecke eines Knotens immer ein kontinuierliches Stück Speicher belegen.
Dieser Algorithmus wird rekursiv auf die Kindknoten angewendet, bis ein bestimmtes Abbruchkriterium erreicht wurde.
Vor jeder Teilung eines Knotens wird überprüft, ob an den Grenzen des Volumes ein leerer Raum besteht. Anhand eines Schwellwertes wird definiert, ab wann dieser leere Raum abgetrennt wird und daraus ein leerer Knoten ensteht oder ob der Knoten normal weiter geteilt wird. Dieser Test ist notwendig, damit die Bounding Boxen der Knoten an die darin enthaltene Geometrie angepasst werden.
Schnitt/Traversierung
Das Traversieren der BIH ist ähnlich zu dem Traversieren der BVH, da es möglich ist leeren Raum zwischen zwei nicht überlappenden Kindknoten zu schneiden. Dennoch profitiert die BIH auch von der räumlichen Aufteilung, da es mit Hilfe der Strahlrichtung möglich ist, direkt das Kind zu traversieren, welches näher am Strahlursprung liegt. Dadurch ähnelt das Traversieren wiederum einem k-d Baum. Da die Knoten der BIH sich überlappen können, ist es nicht möglich sofort bei einem Schnitt mit der Szenengeometrie die Traversierung zu stoppen. Es ist notwendig die restlichen Elemente auf dem Traversierungsstack zu testen, um auszuschließen, dass ein Schnittpunkt existiert, welcher näher am Kameraursprung liegt. Dennoch kann die zu traversierende Struktur reduziert werden, sobald ein Schnittpunkt gefunden wurden, da alle Knoten, welche sich weiter entfernt zur Kamera befinden, als der derzeitige Schnittpunkt, verworfen werden können.
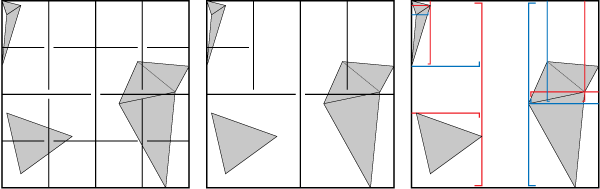
Raytracer
Anstelle des rekursiven Raytracing-Verfahrens nach Whitted wurde ein iterativer Algorithmus entworfen, bei dem Strahlen generationenweise abgearbeitet werden. Der Beleuchtungsanteil jeweiliger Pixel setzt sich zusammen aus dem Beleuchtungsmodell und den einzelnen Strahlenkategorien (Primär-, Reflektions-, Refraktions- und Schattenstrahlen). Die Bildebene wird nach einer Lebesgue-Kurve gerastert, um die Lokalität der Primärstrahlen zu erhöhen. Daraufhin wird für jeden dieser Strahlen ermittelt, ob ein Schnitt mit den einzelnen geometrischen Strukturen der Szene erfolgte. Im Falle eines Schnitts werden abhängig von den Materialeigenschaften Reflektions- und Refraktionsstrahlen sowie Schattenstrahlen entsprechend der Anzahl der Lichtquellen erzeugt. Nach Beendigung eines Durchgangs der Erstellung einer Strahlengeneration durchläuft diese den Shading-Abschnitt. Dafür wird ein Phong-Beleuchtungsmodell unter Zuhilfenahme der Schlick-Approximation verwendet, um eine realistischere Darstellung von metallischen Oberflächen zu erreichen. Strahlen, welche die Szene verfehlt haben, fügen ihren Anteil zur Beleuchtung des Pixels entsprechend eines Environment-Map-Lookup hinzu.
Um Aliasing-Artefakte zu vermeiden, wird, sobald keine Interaktion mit der Szene erfolgt, das Bild nochmals mit minimaler Ablenkung der Primärstrahlen neu berechnet und in einem separaten Puffer abgelegt. Die einzelnen Pixel werden dann aus den Bildern in diesem Puffer gemittelt und angezeigt.
Unterschied zwischen Aliased und Anti-Aliased
Parallelisierung
Der Raytracing-Algorithmus ist prädestiniert dazu, parallelisiert zu werden. Diverse Abschnitte können unabhängig voneinander und simultan ausgeführt werden. Hier wird der Ansatz genutzt, die Bildebene in Kacheln aufzuteilen, von denen eine Untermenge dann parallel abgearbeitet werden kann. Die Parallelisierung wird in zwei Varianten mittels der externen Bibliotheken Boost.Thread und Intel Threading Building Blocks realisiert. Boost.Thread offeriert die Möglichkeit, relativ nah am Betriebssystem das Thread Pool Pattern zu implementieren. Im Gegensatz dazu handelt es sich bei der Bibliothek von Intel um eine High Level Parallelisierungs-Bibliothek, die im Kontrast zu nativen Threading-Paketen einen Großteil der Implementationskomplexität verbirgt und den Mehrprozessorzugriff abstrahiert. Einzelne Algorithmus-Bestandteile werden als Tasks modelliert. Die Allozierung von individuellen Prozessorkernen, Erstellung von eigentlichen Threads und deren Synchronisation, sowie effiziente Nutzung des CPU-Caches übernimmt die Laufzeit-Engine der Bibliothek.
Implementierung
Entwickelt wurde das Framework komplett in C++ für Linux, Windows und Mac OS X.
Resultate
| Name (Dreiecke) | Vier Kugeln (5.452) | Teapot (16.896) | ||||
| BVH | BIH | KD | BVH | BIH | KD | |
| Bauzeit (sec) | 0,07 | 0,52 | 2,17 | 0,23 | 1,66 | 20,05 |
| Knoten | 10.903 | 26.805 | 25.603 | 33.791 | 71.941 | 82.015 |
| Speicherbedarf (MB) | 0,374 | 0,307 | 0,21 | 1,16 | 0,823 | 0,66 |
| Name (Dreiecke) | Lucy (78.870) | Conference (282.094) | ||||
| BVH | BIH | KD | BVH | BIH | KD | |
| Bauzeit (sec) | 1,27 | 7,83 | 592,51 | 3,01 | 12,28 | 168,74 |
| Knoten | 157.739 | 386.781 | 456.693 | 564.187 | 576.579 | 3.952.379 |
| Speicherbedarf (MB) | 5,415 | 4,426 | 3,65 | 10,32 | 6,6 | 31,62 |
| Name (Dreiecke) | Clio (348.397) | |||||
| BVH | BIH | KD | ||||
| Bauzeit (sec) | 5,13 | 25,47 | 741,31 | |||
| Knoten | 696.793 | 1.285.357 | 1.851.887 | |||
| Speicherbedarf (MB) | 23,92 | 14,71 | 14,82 | |||





Fazit

BVH:
+ bekannter Speicherverbrauch
+ sehr schneller Aufbau
- Volumen können sich überschneiden
- Relativ aufwendige Schnittberechnung durch Boxschnitt
BIH:
+ bekannter Speicherverbrauch
+ schneller Aufbau
+ Schnittberechnung mit Ebenen (ähnlich k-d Baum)
- Volumen können sich überschneiden
k-d Baum:
+ keine Volumen überlappung, daher frühzeitiger Traversierungsabbruch bei Schnitt mit der Szene
+ Schnittberechnung mit Ebene
- unbekannter Speicherbedarf (mehrfach Referenzierung)
- Ungenauigkeit durch Gleitkommazahlen
Die durchgeführten Tests zeigen, dass die vorliegende Implementierung nur sublinear skaliert. Erkennbar ist, dass der limitierende Faktor für die Skalierbarkeit nicht die CPU, sondern viel mehr die Bandbreite des Hauptspeichers ist. Der Entwurf des Datenlayouts der Strahlengenerationen und Beschleunigungsstrukturen zielt darauf ab, möglichst hohe Effizienz bei der Auslastung der Cachelines zu schaffen, kann aber noch weiter verbessert werden. Als vielversprechend bezüglich der Performancesteigerung dürfte sich die Verwendung der SIMD-Erweiterung für Vektor- und Matrix-Operationen, sowie der Einsatz eines Packet-Raytracing-Algorithmus, bei dem Strahlen paketweise bearbeitet werden, erweisen.
Ausblick AS-RTRT 2
In der Fortführung des Projektes wird das erworbene KnowHow genutzt um einen Raytracer auf der GPU für dynamische Szenen zu erschaffen. Dabei soll das die Erstellung der Beschleunigungsstruktur als auch das Rendern auf der GPU vollzogen werden.
Material
- Zwischenpräsentationen: Bounding Interval Hierachy
- Endpräsentation
- Projektseite
Referenzen
- I. Wald:
On fast Construction of SAH-based Bounding Volume Hierarchies
Proceedings of the 2007 Eurographics/IEEE Symposium on Interactive Ray Tracing, 2007. - A. Williams, S. Barrus, R. K. Morley, P. Shirley:
An Efficient and Robust Ray-Box Intersection Algorithm
Journal of Graphics Tools, 2003. - C. Wächter, A. Keller:
Instant Ray Tracing: The Bounding Interval Hierarchy
IN RENDERING TECHNIQUES 2006 - PROCEEDINGS OF THE 17TH EUROGRAPHICS SYMPOSIUM ON RENDERING, 2006. - T. Möller, B. Trumbore:
Fast, minimum storage ray-triangle intersection.
Journal of Graphics Tools, 2(1):21--28, 1997. - V. Havran, R. Herzog, H.P. Seidel:
On the Fast Construction of Spatial Hierarchies for ray Tracing.
Proceedings of the 2006 IEEE Symposium on Interactive Ray Tracing, pp. 7180 (September 2006). - I. Wald, V. Havran:
On building fast kd-trees for Ray Tracing, and on doing that in O(N log N).
Proceedings of the 2006 IEEE Symposium on Interactive Ray Tracing, 2006, pages 61-69.
