| Line 139: | Line 139: | ||
3 g:2 died 375.58804 65.089584 : 175 30 c: 7 8 | 3 g:2 died 375.58804 65.089584 : 175 30 c: 7 8 | ||
...</pre> | ...</pre> | ||
<gallery widths=300px heights=300px mode="packed-overlay"> | |||
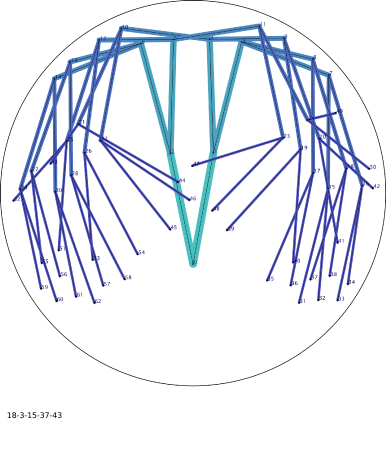
Image:Img_18-3-15-37-43.png|Connection lines between (dead) fish of 6 generations | |||
</gallery> | |||
== Parameters and Variations == | == Parameters and Variations == | ||
Revision as of 18:09, 2 April 2015
Felicitas Höbelt
Github
My repo is here.
Final Project Documentation
Principia Textilica
Context
In the course “Principia Textilica” we explore intersections of computational algorithms and textile craft, including pattern generation algorithms, weaving techniques, knot theory, hands-on experience with textile maschines, history lessons and more. For the final project each student is encouraged to find a subject to implement some of the methods and techniques we see during the course.
Motivation
I study Computer Science and Media, which means my background is more algorithmic and technical than art-related. Nevertheless, I am familiar with a few textile techniques such as knotting (Macramé), weaving, sewing, felting and embroidery.
For inspiration I look at two topics that have fascinated me for years: Modeling “Living” Things (plants/fungi/insects/animals) and complexity.
Complexity is often mistaken for complicatedness because the result looks complicated. However, most systems that produce complex results are very simple. It consists of a certain number of elements and a few elemantary rules which are applied to those elements.
My goal is to use both, complexity and modeling simple “life”, to create a textile pattern.
Idea
The Pond/Fish Tank
I will use a swarm model, which means I have a number of individuals which are controlled by a set of rules concerning themselves, their dynamic environment (e.g. the other members of the swarm) and their static environment (e.g. boundaries of the tank). The metaphor I choose is a school of fish moving around in a pond or glass tank.
The desired pattern will be generated by the movements of the individuals. I want to start with the rules and successively adapt them depending on the outcome.
I do not want to settle for a specific textile technique at this point, but I know I want to assign a thread to each of the individuals. With this premise in mind, favourable textile techniques are embroidery and knotting.
Rules
My fish program is in 2D and has two main elements: the tank and the fish.
The tank started out as rectangular, but I find a circle to be more aesthetically pleasing as well as more fitting for an embroidery hoop. The circle embodies the simple inside/outside world that I need.
The basic swarm rules below share some similarities with the “Boids” program by Craig Reynolds[1]. He developed an agent-based algorithm to simulate the flocking behaviour of birds.
There is no randomness in my program. The behaviour of the fish is essentially determined by three basic principles:
- Company
- Each fish will follow other fish.
- Privacy
- Each fish needs a minimum of private space.
- Boundary
- Each fish will stay inside the tank.
as well as two optional principles:
- Security
- Each (non-predatory) fish will avoid any predators.
- Mortality
- Each fish can have children. Fish can die of childbirth.
Implementation
For implementing my idea I use Processing 2.0[2], because I am already familiar with Java. Also Processing is one of the tools we use during the course, so all participants know how to look into my code and adapt it if they want to.
This section will focus more on algorithms and data flow rather than implementation details. There are four ways of running the program represented by the combination of optional mechanisms on top of the basic ones:
- use both Security and Mortality
- use only Security
- use only Mortality
- use none of them
It is worth noting that the code still includes all methods and parameters that I do not use for the textile piece or the parameter variations, but I will restrict the explanations to the version I actually use (3. only Mortality). In this version each fish will have two children when it dies. The resulting pattern is made of straight lines connecting parents with their children. The movement of the fish is influenced by all living fish as well as all dead fish. I start with one fish and stop at 6 or 7 generations.
Algorithm
| Class | responsible for |
|---|---|
Exporting the Values
To be able to extract all important positions and values from the program several logging methods are implemented. The program produces a simple text-file, where the parameter values are noted as well as the positions of the fish (original coordinates plus coordinates scaled to fit the textile application), their id and their children. The tank class produces an image where the positions of the fish are noted pixelwise, the image shows their complete movement. I also export an SVG-file with a straight line connecting the end position of each fish with their children. This export can be done with additional text output directly within the SVG-file (the id of each fish above its “grave”).
The text-based log file (example below) consists of all important parameters as well as the coordinates of each fish, g: denotes the generation while c: denotes the ids of its descendents.
tank cx,cy,radius: 300.0 300.0 300.0 starter fish: 1 start dir: 0.0 -1.0 start pos: 300.0, 300.0 wall/neighbor 0.9/0.1 maxGenerations 6 maxChildren 2 spawnTime 6000ms spawnAnglesDegree 135.0 -135.0 turnSpeed 0.011/ms private radius / company radius 30.0 / 70.0 fish: 0 g:0 born 300.0 590.0 : 140 275 c: 0 g:0 died 300.0 410.82532 : 140 192 c: 1 2 1 g:1 died 331.64142 237.63405 : 155 111 c: 3 4 2 g:1 died 264.66016 238.89192 : 124 111 c: 5 6 3 g:2 died 375.58804 65.089584 : 175 30 c: 7 8 ...
Parameters and Variations
There are several more, but some of the most important fish parameters and properties are:
- privateRadius
- If another fish is within this distance (in pixel) the current fish moves away from it.
- companyRadius
- If another fish is within this distance (in pixel) the current fish imitates the other fish’s movement (linear interpolation between current direction vector and target direction vector).
- interpolationSpeed (related to speed of turns)
- This value is the number of milliseconds which are needed to reach the target vector with linear interpolation. Since interpolation is mainly used when a fish changes its direction vector the interpolationSpeed is inversely related to the speed of turns.
- timetoSpawn
- This is the life span of one fish (in milliseconds), in the moment of dying it will generate two new fish.
- spawnAnglesDegree
- This array contains the angles (in degrees) for the initial direction of each child (relative to the parent’s direction).
When varying one parameter the others are set to a default value to cleanly separate the effects of the change. The “baseline” setting with all parameters set to default is included in each of the variation series. The natural order of the parameter sizes detemines its placement within the series (ordered by increasing values). Table [table:variation] shows the used integer values.
| Parameters | Default value | Variation |
|---|---|---|
| privateRadius | 30 | 20 30 40 50 |
| companyRadius | 70 | 50 70 90 120 |
| interpolationSpeed | 100 | 50 100 150 200 250 350 |
| timetoSpawn | 6000 | 3000 4000 5000 6000 8000 |
| spawnAnglesDegree (+/-) | 135 | 0 20 45 90 135 180 |
[table:variation]
The following images show the different outcomes for variations of the parameters. On the left you see the connections between related fish, on the right there are their movement traces (actual paths).
Variations of “privateRadius”
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image [privateRadius50]
[t]0.46
Variations of “companyRadius”
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
Variations of “interpolationSpeed”
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image [interpolationSpeed350]
[t]0.46
Variations of “timetoSpawn”
[t]0.46 image [timetoSpawn3000]
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
Variations of “spawnAnglesDegree”
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
[t]0.46 image
[t]0.46
Textile Implementation
Thoughts on Goals
Throughout the whole development of the algorithms and parameter variations I played with several ideas on how to go from digital to textile. The basic idea was to use threads as entities or individuals. However, I was very indecisive about the details. Early ideas included just embroidering the movement of the fish or use the movements to (pseudo-) weave. I also came up with a Macramé-related knotting scheme, that resembled an RPG: each thread could win or lose in a fight against other threads.
None of those concepts are interesting enough for me. All of them have a building or producing element in common, so I tried to turn that element upside down. Working with textiles is usually constructing something. Howerever, there will be steps you have to reverse, because you made a mistake or the material was flawed. You have to untie the knot, unweave your cloth or just untangle the mess. Yet these unwanted destructive processes happen in favor of the final product.
I want to exaggerate the principle of destruction for my textile piece. Still adhering to the threads as individuals it means deconstructing the elements itself: one thread contains other, thinner threads and fibers. The parent-child-relation between the fish in my tank fits in seamlessly with the construction-by-deconstruction-concept. The parent fish contains all the material needed to form the children, which then again contain everything for their children.
I will use a thread and split it up into subthreads, which match the connection between parent and children.
Textile Piece I
Method and Tools
[t]0.48
[t]0.48 For my first practical trial run I use evenweave with approximately 2mm per unit. To limit the size I scale down the computed positions to fit a 100 by 100 grid (resulting in appr. 20cm by 20cm for the finished piece). The yellow thread is used as a counting help.
[t]0.48
[t]0.48 Because my generations of fish are based on the number 2, I also need thread based on number 2. So I use cotton wool threads each already containing 8 (<math>=2^3</math>) sub-threads when feazed.
To be able to manage the threads and associate them with one fish id I simply attach some paper to the string groups. The positions are directly read from the text in the log file.
[t]
tank cx,cy,radius: 300.0 300.0 300.0 starter fish: 1 start dir: 1.0 1.0 start pos: 300.0, 300.0 wall/neighbor 0.9/0.1 maxGenerations 7 maxChildren 2 spawnTime 5000ms spawnAnglesDegree 135.0 -135.0 turnSpeed 0.0051/ms private radius / company radius 40.0 / 75.0 fish: 0 g:0 born 300.0 300.0 : 140 140 c: 0 g:0 died 409.58185 409.58185 : 191 191 c: 1 2 1 g:1 died 434.7048 547.7104 : 203 256 c: 3 4 2 g:1 died 547.1275 435.0458 : 255 203 c: 5 6 3 g:2 died 299.06696 479.5542 : 140 224 c: 7 8 4 g:2 died 290.70502 579.7467 : 136 271 c: 9 10 5 g:2 died 578.5094 290.45987 : 270 136 c: 11 12 6 g:2 died 474.91296 301.06262 : 222 140 c: 13 14 ...
[t]0.46 image
[t]0.46 image
[t] image [trial1]
Result
The left of Fig.[trial1] shows the state of the first experiment when it is apparent I am not getting anywhere near to what I wanted. One reason is a simple mistake in determining the thread count: For 7 generations I actually would only have needed <math>2^6</math> instead of <math>2^7</math> single threads in the end, because I forgot to start counting at <math>2^0</math>. This would have reduced the thickness of the starting thread by half and also changed the appearance significantly.
A more serious problem for me is that the visual outcome is somehow off. Maybe I chose the evenweave’s units too large or the wrong color, but most importantly the intermediate result does not have the properties I expected it to have: it is neither 2D nor 3D, neither are the threads stiff and straight enough for the connections of the fish nor do they show the actual movement of a fish during its life cycle. This first piece is an unsatisfying accumulation of imprecise craftsmanship, so I have to find other possibilities to work with the pattern in the material world.
Textile Piece II
Method and Tools
Unlike techniques such as stitching or weaving where the interaction between up and down movements is crucial, the destruction concept I want to explore is independent from that. That means I need a more robust canvas. I use a non-textile base, namely a semi-see-through PVC sheet. Although it is possible to cut holes in the PVC for guiding the threads, as said before, this would artificially add something to the concept that does not belong to it. Instead, a hot glue gun is used to fixate the splitting points and keep the strings neatly in place. Pieces of a series can be stacked and the viewer can easily compare the different layouts of the strings.
For the threads I use the same type of cotton wool as with experiment number one (in white instead of blue), but only 6 generations, meaning <math>2^5 = 32</math> sub-threads which equals 4 of the normal threads. The wool is hand-dyed to achieve a color gradient from dark blue to green to yellow to white, which aids the visual understanding of distinct generations. The dying process makes it more difficult to feaze the threads.
Result
[t]0.46 image
[t]0.46 image
There are four templates for the finished pieces, including the default setting, which are described under Fig .[privateRadius50], Fig. [interpolationSpeed350] and Fig. [timetoSpawn3000]. I am satisfied with the result, as it fulfills the goals I set before. There are definitely alternatives for the fixation method, but at this point the glue dots, which are quite visible despite being transparent, act as subtle placeholder for the fish bodies. Additionally, while working with the threads, some aspects emerged that I did not actively take into account in the planning phase. The first is the overlapping of the threads, naturally falling into place if the correct order of the fish births and deaths is maintained. The second is the color imperfection as a result of the (amateur) hand-dying. The dye did not touch any fibers below the surface of the initially whole thread, as a consequence the feazed threads partly stayed white. Both aspects fit beautifully into the whole concept, the latter one especially adds another element to the destructive dimension.
Conclusion
We see crafting usually as a process of creation, building, fixing and making. But most crafting techniques have destructive aspects in between: we cut fabric into pieces before sewing and we remove excess threads when knitting. I started with an artificial, minimal life form, that moves, gives birth and dies and interacts with the other life forms in a complex way, based on a set of simple rules. I explored variations of the rules and observed changes in the complex behaviour of the life forms, developping both expected and surprising features as outcome. Then I turned its heritage into a destructive textile piece, where I consciously nullified the effort of making a thread from several fibres, by feazing and dissecting it.