| Line 151: | Line 151: | ||
==Irreführende Darstellungen== | ==Irreführende Darstellungen== | ||
Diagramme können Daten auch verzerrt darstellen. Selbst wenn die Zahlen alle korrekt sind, können Daten so dargestellt werden, dass die den Eindruck vermitteln das Werte größer oder kleiner sind als in Wirklichkeit. Das ist die negative Kehrseite davon, dass Diagramme meist einfacher und schneller verständlich sind als Zahlen. | Diagramme können Daten auch verzerrt darstellen. Selbst wenn die Zahlen alle korrekt sind, können Daten so dargestellt werden, dass die den Eindruck vermitteln das Werte größer oder kleiner sind als in Wirklichkeit. Das ist die negative Kehrseite davon, dass Diagramme meist einfacher und schneller verständlich sind als Zahlen. | ||
===Beispiele für Verzerrende Darstelungen=== | |||
===Achsen verzerren=== | ====Achsen verzerren==== | ||
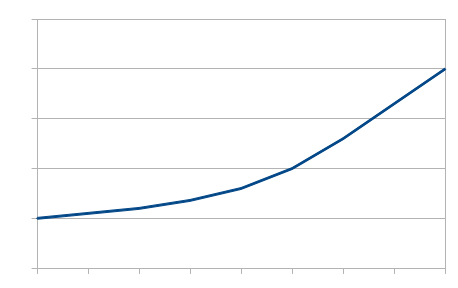
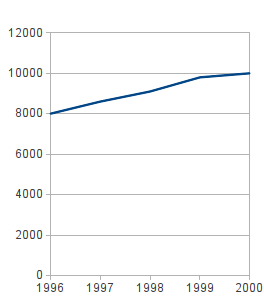
* die Achsen länger gemacht werden (Unterschiede wirken größer) [[File:CourseVisualisation_ComparsionLengthendAxis.png]] | * die Achsen länger gemacht werden (Unterschiede wirken größer) [[File:CourseVisualisation_ComparsionLengthendAxis.png]] | ||
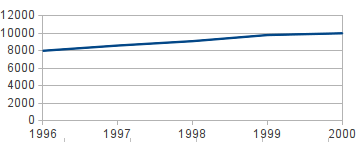
* Die Achsen gestaucht werden (Unterschiede wirken kleiner) [[File:CourseVisualisation_ComparsionShortenedAxis.png]] | * Die Achsen gestaucht werden (Unterschiede wirken kleiner) [[File:CourseVisualisation_ComparsionShortenedAxis.png]] | ||
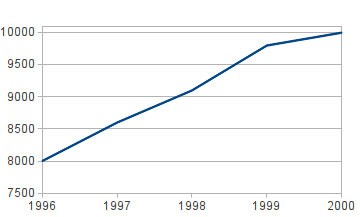
* Die Achsen nicht bei 0, sondern bei einem anderen Wert beginnen (Unterschiede wirken größer) [[File:CourseVisualisation_ComparsionCutAxis.png]] | * Die Achsen nicht bei 0, sondern bei einem anderen Wert beginnen (Unterschiede wirken größer) [[File:CourseVisualisation_ComparsionCutAxis.png]] | ||
===Grafiken irreführend skalieren=== | ====Grafiken irreführend skalieren==== | ||
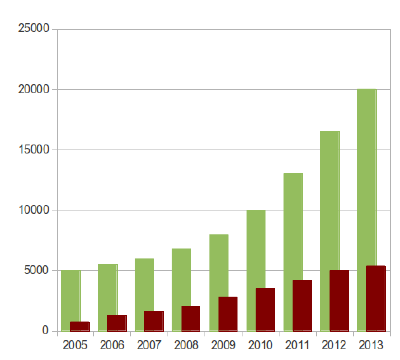
Statt Balken Grafiken verwenden, bei denen die Höhe der entscheidende Wert ist, aber Höhe und Breite skaliert werden. Dadurch das die Höhe linear ansteigt, aber die Fläche quadratisch… [[File:CourseVisualisation_ComparsionScaledVsMultiple.png]] | Statt Balken Grafiken verwenden, bei denen die Höhe der entscheidende Wert ist, aber Höhe und Breite skaliert werden. Dadurch das die Höhe linear ansteigt, aber die Fläche quadratisch… [[File:CourseVisualisation_ComparsionScaledVsMultiple.png]] | ||
===Nicht-3-D-Daten in 3D darstellen=== | ====Nicht-3-D-Daten in 3D darstellen==== | ||
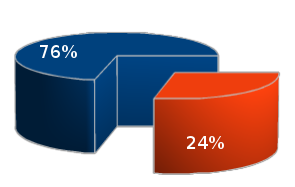
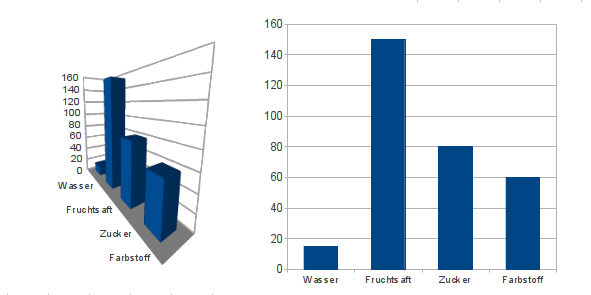
Durch die Perspektive werden die Daten verzerrt: Was näher ist, wirkt (auch zahlenmäßig) größer; Zudem werden überflüssige graphische Elemente eingefügt. | Durch die Perspektive werden die Daten verzerrt: Was näher ist, wirkt (auch zahlenmäßig) größer; Zudem werden überflüssige graphische Elemente eingefügt. | ||
[[File:CourseVisualisation_Comparsion3D2D.png]] | [[File:CourseVisualisation_Comparsion3D2D.png]] | ||
==Aufgabe== | ==Aufgabe== | ||
Revision as of 17:45, 31 July 2013
Warum Diagramme?
Visualisierungen oder Diagramme sind dir vielleicht aus der Zeitung oder aus den Nachrichten bekannt: Wie die Wirtschaft einen Landes wächst, oder der Wert eines Unternehmens ist, wird oft als eine Linie dargestellt: Sie steigt an, wenn der Wert größer wird und fällt, wenn der Wert sinkt. Diese Darstellungen basieren auf Zahlen, die gemessen werden – z.B. durch Aktionverkäufe an der Börse. Dadurch wird festgestellt wie viel Wert eine Aktie hat und dieser Wert wird dann in ein Diagramm umgewandelt.
Wenn aber Diagramme auf Zahlen basieren, warum solltest du daraus ein Diagramm erstellen wollen? Schliesslich ist es zusätzliche Arbeit und die Zahlen sind das genauste was du hast!
Stell dir vor, du bist bei der Limonadenfirma SipIt angestellt. Du willst wissen, ob die Firma wächst und Jahr für Jahr mehr Limonadenflaschen verkauft. Dazu hast du diese Zahlen, die zeigen, wie viel die Firma verdient. Du wüsstest auch gerne, ob die Firma im Vergleich zur Konkurrenz, der Firma CHUCKthat gut ist –
| Firma | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| SipIt | 150000 | 160000 | 165000 | 180000 | 210000 | 215000 | 210000 | 230000 | 220000 | 220000 | 240000 | 245000 | 250000 | 260000 |
| Chuck-that | 200000 | 230000 | 235000 | 245000 | 245000 | 260000 | 275000 | 294000 | 305000 | 260000 | 240000 | 220000 | 225000 | 230000 |
Gewinn (in €) pro Jahr
Aufgabe:
- Welche Firma macht momentan mehr Gewinn?
- Welche Firma ist in den letzten Jahren am stärksten gewachsen?
- Du hast die Zahlen genutzt um festzustellen, wie sich die Firmen entwickelt haben. Was wären Vor- und Nachteile, wenn du die Zahlen nun visualisierts, also z.B. ein höheres Ergebnis durch einen höheren Balken darstellst?
- Um den Unterschied einer Visualisierung als Diagramm auszuprobieren, erstelle ein Linien-Diagramm aus den Zahlen in der Tabelle!
| ' | Januar | Februar | März | April | Mai | Juni | Juli | August | September | Oktober | November | Dezember |
| Limo | 5000 | 4800 | 6000 | 9000 | 14000 | 20000 | 30000 | 32000 | 20000 | 10000 | 4000 | 4000 |
| Kakao | 8500 | 7500 | 5000 | 4500 | 2000 | 1100 | 1000 | 1200 | 1500 | 2000 | 4000 | 8000 |
Getrunkene Liter des Getränkes pro Monat.
Du kannst z.B. Diagramme mit Programmen wie Excel, Calc oder Illustrator erstellen. Du kannst ein Diagramm auch mit Stift und Lineal zeichnen.
Was kannst du aus den dargestellten Daten schliessen?
Diagrammtypen
Es gibt verschiedene Arten von Visualisierungen. Hier eine Übersicht.
Liniendiagramm
Der Zusammenhang von 2 Merkmalen kann in Linienform dargestellt werden, wobei der eine Wert an der Horizontalen, der andere an der Vertikalen eingetragen wird. Beide Werte sollten kontinuierlich sein und keine Kategorien. Kontinuierlich ist z.B. das Einkommen oder die Körpergröße, Kategorien sind Beruf oder Land.
Beispiel für die Verwendung: Menge an getrunkenem Bier zu gelaufener Strecke ohne hinzufallen
Balkendiagramm und Sauelendiagramm
Zusammenhang von 2 Merkmalen. Eines der beiden Merkmale sollte eine Einteilung in Kategorien haben, das andere kontinuierlich sein. Das Balkendiagramm stellt dabei Datenreihen als waagerecht liegende Balken dar, und das Saeulendiagramm als nebeneinander aufgereihte senkrechte Sauelen.
Beispiel für die Verwendung: getrunkene Liter verschiedener Limonadensorten
Kuchendiagramm
Ist die Darstellungsform für Teilwerte eines Ganzen als Teile eines Kreises. Wird häufig zur Darstellung von Verteilungen und Anteilen genutzt. Um jeweilige Sektoren leicht zu unterscheiden, kann man Farbe, Muster oder Schattierungen verwenden. Kuchendiagramme sollten nur zur Angabe von Prozentwerten und Anteilen verwendet werden.
Nachvollziehbarkeit
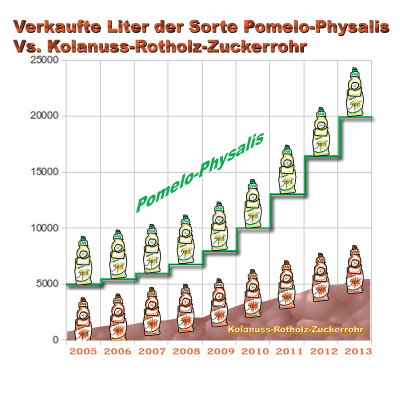
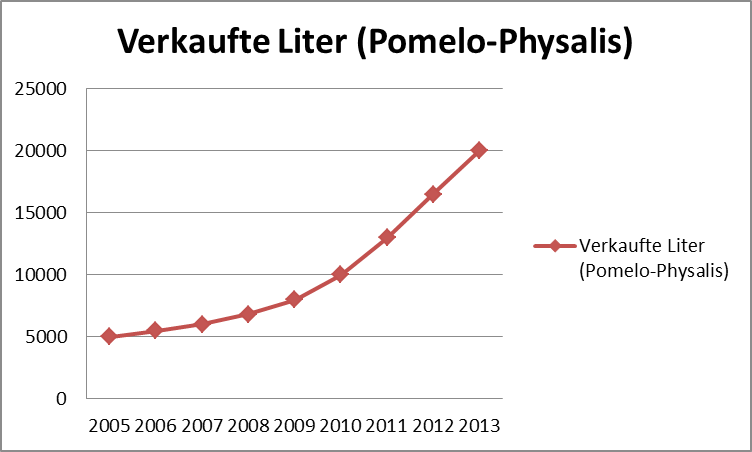
AUFGABE: Ihr kauft von einem Handelspartner Pomelos für eure neue Sorte Pomelo-Physalis. Ihr habt ihm ein Diagramm gesendet, das zeigen soll, dass der Verkauf dieser Sorte sehr gut läuft. Leider sagt er, er kann mit dem Diagramm nichts anfangen. Weißt du Warum?
Ohne eine klare Beschriftung ist nicht klar was das Diagramm überhaupt darstellt. Deshalb solltest du deine Diagramme beschriften:
- Was wurde gemessen?
- In welcher Einheit?
- Was für ein Zusammenhang wird in dem Diagramm dargestellt?
Aufgabe: Das sind die Orignaldaten
Verkaufte Liter der Sorte Pomelo-Physalis
| Jahr | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Verkaufte Liter | 5000 | 5500 | 6000 | 6800 | 8000 | 10000 | 13000 | 16500 | 20000 |
überarbeite das Diagramm für den Verkauf von Pomelo-Physalis-Limo um erschließbar zu machen, was dargestellt ist und wie.
Grafische Gestaltung
AUFGABE: In der Limonadenfirma, für die du arbeitest, gibt es schon ein paar Diagramme. * Eines zeigt, wie sich die verschiedenen Limonadensorten verkauft haben.
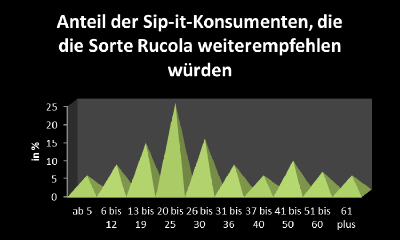
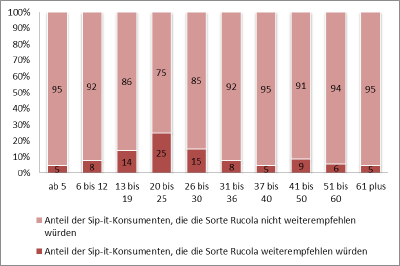
- Ein anderes Anteil der Kunden, die Sip-It weiterempfehlen würden.
Was ist das Problem an diesen Grafiken?
Es ist sinnvoll, eine Visualisierung so einfach wie möglich zu halten. Je mehr von den Daten ablenkt, desto schwieriger ist das Diagramm zu lesen. Eine einfache Regel ist, kein Element einzufügen, das nicht zum besseren Verständnis der Daten beiträgt, bzw. alle Elemente zu löschen, die das Diagramm nicht verständlicher wird.
Aufgabe: Was wäre das in der Grafik oben?
Sehr einleuchtend ist es, die dekorierenden Grafiken loszuwerden. Aber auch scheinbar funktionstragende Elemente können entfernt werden: Das Gittermuster im Hintergrund lenkt vom Inhalt ab und kann zurückgenommen werden.
Aufgabe:
- Gestalte diese Diagramme so um das nur noch Elemente enthält, die zum Verständnis der Daten beitragen.
- Finde Beispiele für Diagramme und diskutieren in der Gruppe, ob die grafische Darstellung dabei hilft die Daten zu verstehen.
Irreführende Darstellungen
Diagramme können Daten auch verzerrt darstellen. Selbst wenn die Zahlen alle korrekt sind, können Daten so dargestellt werden, dass die den Eindruck vermitteln das Werte größer oder kleiner sind als in Wirklichkeit. Das ist die negative Kehrseite davon, dass Diagramme meist einfacher und schneller verständlich sind als Zahlen.
Beispiele für Verzerrende Darstelungen
Achsen verzerren
- die Achsen länger gemacht werden (Unterschiede wirken größer)
- Die Achsen gestaucht werden (Unterschiede wirken kleiner)
- Die Achsen nicht bei 0, sondern bei einem anderen Wert beginnen (Unterschiede wirken größer)
Grafiken irreführend skalieren
Statt Balken Grafiken verwenden, bei denen die Höhe der entscheidende Wert ist, aber Höhe und Breite skaliert werden. Dadurch das die Höhe linear ansteigt, aber die Fläche quadratisch… File:CourseVisualisation ComparsionScaledVsMultiple.png
Nicht-3-D-Daten in 3D darstellen
Durch die Perspektive werden die Daten verzerrt: Was näher ist, wirkt (auch zahlenmäßig) größer; Zudem werden überflüssige graphische Elemente eingefügt.
Aufgabe
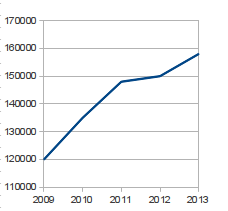
Rechteckige Flaschen scheinen voll im Trend zu sein – behauptet zumindest eine Studie, die euch von einem Flaschenhersteller zugesendet wurde:
Sind die Werte in den Diagrammen korrekt? (vergleiche Tabellendaten).
| Jahr | 2009 | 2010 | 2011 | 2012 | 2013 |
| Verkauf | 120000 | 135000 | 148000 | 150000 | 158000 |
| rund | rechteckig |
| 76% | 24% |
Du erstellst die Grafiken neu, um deinem Chef eine objektive Einschätzung zu ermöglichen, ob auf rechteckige Flaschen umgestiegen werden soll. Wie glaubst du wird er sich entscheiden?