<automata>
Context:
'Life is a simulation' or is it? The quest for finding a set of rules to simulate life in some shape or form has been around for ever. Whether it is in search for the free will or just to find out what makes things living. One mathematical approach got introduced to world in 1970 by the British mathematician John Horton Conway, the Game of Life. The so called Game of Life (or GoL in short) is a 'cellular automaton', a type of simulation that works on a regular grid of cells and in discrete time-steps. For every time-step a set of rules is enforced for every cell, determining it's state. In most cellular automaton there are only two states 'living' and 'dead'. Depending on the rules and other constrains of the simulation, complex patterns might occur and this project will try to take these patterns and represent them as notes in a 'cellular automaton synthesizer'.
cellular automaton in different dimensions
Concept:
For this project I will use a one-dimensional or so called elementary cellular automaton, represented as a line of 32 cells. In every time-step of the simulation the state of the cell (living or dead) is considered and than the state of the two neighboring cells, edge-cells will be wrapped around. Living cells will be represented as black and dead cells as white pixel. Rules are encoded by all of the possible combinations of the dead cell itself and its neighboring (2^3 = 8). To represent the rules, they are encoded in one-bit-array of length eight like the following graphic illustrates.
[[File:rules.png|800px]
One rule-set and its representation
With theses 8-bits there are 256 possible combinations of rules that can be used for the simulation, these rules often form reoccurring patterns that will be important later.
Some elementary cellular automaton rules and their pattern
To interpret the simulation as music in every time-step the current line of the simulation is read and the different cells interpreted as notes in a musical scale. To minimize dissonance a anhemitonic pentatonic scale is used. Because there are only five notes per octave and no semitones in a pentatonic scale, they produce a simple harmonies that work well with random, pseudo-random and chaotic but structured input.
Different penatonic scales and the matching notes
Approach:
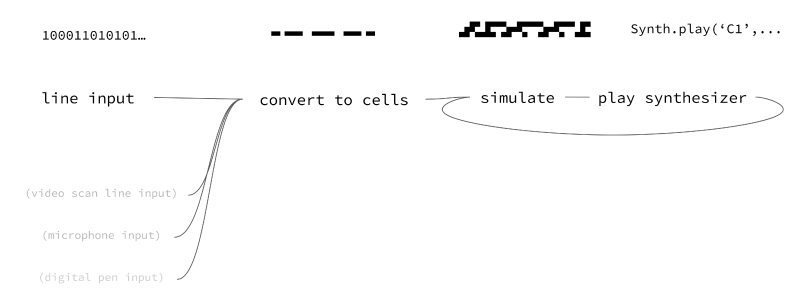
The synthesizer works like the following, the cellular automaton is simulated using the selected rule-set. The current state or line of the automaton is than read from left to right and the matching notes of the selected pentatonic scale played (low notes left, high notes right). To give the user more control over the sound, the notes are split up into eight channels of differing pitch.
One simulation step visualized
The synthesizer is web-based using HTML, CSS and JavaScript. To play notes the library Tone.js (js/tone.js)and their default synthesizer is used (js/synth.js). The simulation is visualized using the Canvas-Api and simulated using native JavaScript (js/automata.js). The User-Interface is written in HTML and CSS (index.html) using onclick-event handlers to interact with the simulation (js/gui.js).
The final synthesizer-ui
Further Reading:
Elementary Cellular Automaton: http://mathworld.wolfram.com/ElementaryCellularAutomaton.html http://atlas.wolfram.com/01/01/rulelist.html https://plato.stanford.edu/entries/cellular-automata/supplement.html
Pentatonic Scale: https://en.wikipedia.org/wiki/Pentatonic_scale https://www.piano-keyboard-guide.com/pentatonic-scale.html
Web Stuff: https://developer.mozilla.org/de/docs/Web/API/Web_Audio_API https://developer.mozilla.org/de/docs/Web/HTML/Canvas https://tonejs.github.io/
Downloads
File:Just open index.html with a modern browser automata.zip