Cellular Automata, Game of Life and Universal Computation
Game of Life
Life, along with this “Game of Life”, is simply a mathematical model of a self-replicatable machine. It was named “Game of Life” since the rules of the game are similar to life of an organism although over-simplified.
“Game of Life” "is played on a theoretically infinite, 2 dimensional square grid where each cell of the grid can take one of two states: “Alive” or “Dead”. The game requires the player to put in an initial pattern of living and dead cells and a program, following some rules, computes the next generation of the pattern."(Nilangshu Bidyanta, 2010) The standard rules of Life are:
- Any live cell with less than 2 live cells in the surrounding 8 cells will die (loneliness)
- Any live cell with more than 3 live cells in the surrounding 8 cells will also die (overcrowding)
- Any live cell with 2 or 3 live cells in the surrounding 8 cells will continue to live to the next generation
- Any dead cell with exactly three live cells in the surrounding 8 cells will come alive (reproduction)
(Nilangshu Bidyanta, 2010)
A very good program for exploring and playing with cellular automata including “Game of Life” is “Golly”. Click the link to learn more and download the proper version according to your operating system. "Operating it is as simple as using Paint program, and it make things much easier to procure the numerous generations. The default pen tool is used to draw new cells or mark alive cells dead. You can also change the speed at which each generation is computed."(Nilangshu Bidyanta, 2010)
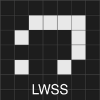
After you've been familiar with Golly and tried it with random patterns or the ones found in the left panel, you would have noticed that some of the patterns occur frequently. "The patterns which remain still for all subsequent generations are called 'Still Lives'. Examples include the “Block” and the “Beehive”. Some patterns moving across the field at different speeds and directions are called spaceships. The smallest spaceship is known as the “Glider”. The “LWSS” is short for “Light Weight Space Ship”. Other patterns repeat after certain generations while maintaining their positions. These are called oscillators."(Nilangshu Bidyanta, 2010) The “Blinker” and the “Beacon” are the most common oscillator.
Golly Ticker
"The more complex patterns must be constructed from a set of basic patterns." (Nilangshu Bidyanta, 2010) The “Golly Ticker” is also no exception. Let’s see what it does first.
Load it from under the menu 'Patterns/Life/Guns/golly-ticker.rle' in the left panel and play it. "You should see the word “Golly” (with a stylized “o”) move across the screen and then disappear at the left. This process continues infinitely," (Nilangshu Bidyanta, 2010) just looks like a stock ticker.
"First, let's start with the Life objects that make up the text "Golly". The text is made up of what is known as the “Light Weight Space Ship” or LWSS for short. These Life objects continuously move in one of the four directions — up, down, left or right but never diagonally. Their speed is often expressed as a fraction of “c” or the speed of light. The speed of light taken in the context of Life refers to advancement of one cell per generation and this is the fastest a Life object can move." (Nilangshu Bidyanta, 2010)
"The “Glider” (mentioned above) can move only diagonally at c/4 whereas the LWSS can move orthogonally at c/2. We can easily verify this using Golly, running slowly enough to clearly see the movements of each generation." (Nilangshu Bidyanta, 2010)
"Each letter is 9 LWSSs in height, except for the "O" which is 11 LWSSs in height. If you take a close look at the characters, not all LWSSs are in the same phase. Some seem to "point" downwards and the rest upwards." (Nilangshu Bidyanta, 2010)
"At the left end, there are structures called "Eaters" or “Fishhook". Just flanked one either side by them are the patterns known as "Kok's Galaxy"." (Nilangshu Bidyanta, 2010)
"Eaters are “Still Lives” which can eat away many objects without sustaining permanent damage. The job of the eater here is to assimilate the LWSSs coming in from the right. Since we have two distinct phases of LWSSs, the eater must be oriented properly to perform its job, otherwise the LWSSs will permanently destroy the eater." (Nilangshu Bidyanta, 2010)
"Kok's Galaxy belongs to the class of oscillators. Functionally, the generations of Kok's Galaxy flanking the eaters don't serve any purpose since deleting them doesn't affect the ticker at all." (Nilangshu Bidyanta, 2010)
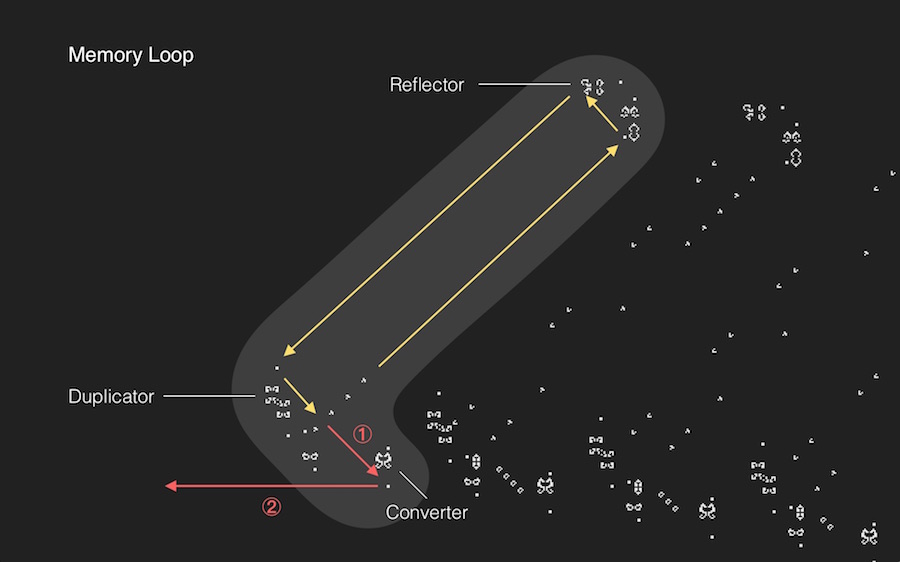
The text is generated row by row. "It starts by first creating the rows in the middle — the sixth and seventh rows. Rows 1 to 6 are created by the six structures at the right-top which are called “memory loops”. The other five are created by the five memory loops at the right bottom. The memory loops hold a specific pattern made of gliders that keep looping in the structure. At one end, they are duplicated where one glider is fed to the "Converter" and the other back into the memory loop." (Nilangshu Bidyanta, 2010)
"The gliders loop following the yellow arrows with the help of “Reflectors” placed at either ends. Additionally at the bottom end there is a glider duplicator. It produces a glider that moves parallel to the original. While the duplicated glider is sent back into the loop, the original glider is sent to a “Converter” which converts the glider to a LWSS (moves along the first red arrow). Following conversion, the LWSS takes the path of the second red arrow, to become one pixel of a row. All of the memory loops work in the same way and are slightly displaced in height to produce LWSS in separate rows." (Nilangshu Bidyanta, 2010)
Modified Golly Ticker & How To
After figuring out the whole functioning mechanism of the “Golly Ticker”, We are ready to modify it to display the text that we want. It’s already quite clear, the key point to get desired output characters is to place the gliders inside each of the memory loops properly, and taking care of the appropriate spacing between gliders. The orders of gliders will be row by row reflected by the replacing LWSS outside. The length of the text to be displayed depends on how many gliders are there in one memory loop, which could be called the memory capacity of the loop.
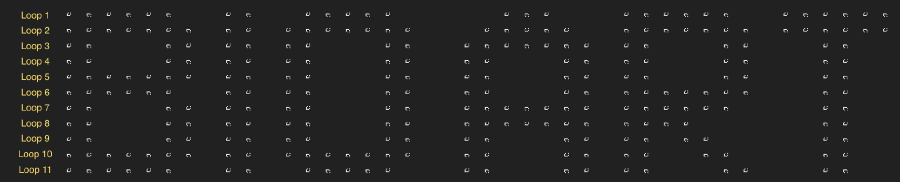
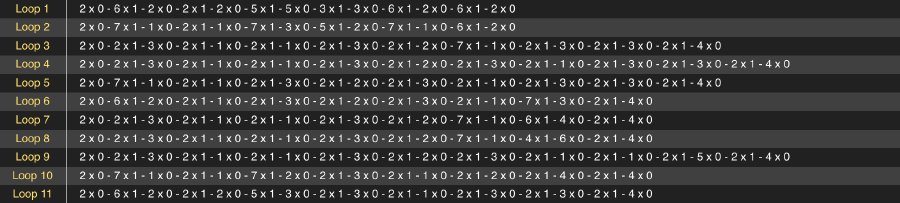
Let’s just get started to place the gliders. I want it to display the text “Bio Art”. The first step that I did is to figure out how these words look like in the final output. Only through this kind of reverse development can we get the exact position of all the gliders in the memory loops. So I drew out the text in 9 lines height. And then for convenience of the later manipulating, I converted the dot matrix pattern into a table of numbers. “1” stands for exist, “0” stands for empty.
With the help of the table generated above, the next step is to transform the codes into the real glider patterns. Rather than “place” them, actually I did the thing of “delete”. I made a default ticker template first, in which each memory loop is full. Now the job becomes easier, I only need to delete the appropriate gliders and temporary eaters according to the table.
We can see that the whole text is generated firstly in row 6 and 7. So it’s where should be started with. Afterwards row 5 and 8 and so on. But the tricky thing is, the next pair of memory loops is always 5 gliders delay than the former one, which means the start points of loop 6 & 7 are different from loop 5 & 8.
Placing the gliders in the appropriate positions and phases in the memory loop involves a lot of trial and error, especially I’m new to the 'Game of Life'. Proper timing is very important. But finally I made it, which came out to be a piece of quite nice artwork. When you zoom in and zoom out to observe this system while it’s running, you may have the illusion that it is alive. At least I’m touched with this tiny, exquisite universe.
Here is a video clip showing how it works
Download the ticker template: File:TickerTemplate.zip
Download my customized ticker in the video: File:CustomizedTicker.zip
Game of Life and Universal Computation
"It is possible for gliders to interact with other objects in interesting ways. For example, if two gliders are shot at a block in just the right way, the block will move closer to the source of the gliders. If three gliders are shot in just the right way, the block will move farther away. This "sliding block memory" can be used to simulate a counter." (Xiphias Press, 2016)
"A sliding block memory pattern was constructed by Hickerson, 1990. It uses several constructions which generate gliders at intervals of 120 generations. This is based on the period 30 Gosper gun. These guns fire salvoes of gliders at a block. The sliding block memory uses a salvo of two gliders to decrement the counter by moving it diagonally one space closer. Three gliders are used to increment it by pushing it further away. An additional glider is sent across the pattern during the decrement. This is deleted by the decrement operation when the block is decremented to zero."
(Paul Rendell, 2015)
"It is possible to construct logic gates such as AND, OR and NOT using gliders. It is possible to build a pattern that acts like a finite state machine connected to two counters. This has the same computational power as a universal Turing machine, so the Game of Life is theoretically as powerful as any computer with unlimited memory and no time constraints: it is Turing complete." (Xiphias Press, 2016)
Paul Rendell has implemented a Universal Turing Machine in Conway’s Game of Life in 2010. The upper picture shows the pattern of it. The lower Figure shows the general scheme of this Turing Machine.
"The finite state machine part can clearly be seen as the square pattern in the bottom left of the picture. This has an addressing mechanism on the left (state value) and at the bottom (symbol value) and nine memory cells to hold the data table to describe the action for each combination of the internal state and symbol values." (Paul Rendell, 2011)
"The Turing Machines tape is represented by the two stack mechanises seen extending top left and bottom right. Each stack cell can trap 3 gliders using the kickback reaction. This is the reaction that turns a glider through 180 degrees when encountering another at right angles. The traps can be seen as empty rectangles between the denser patterns in the cells. These denser patterns delay the transit of the gliders from one cell to the next so that the destination cell is empty when they arrive. The control signals for the cells travel up the sides of the stack." (Paul Rendell, 2011)
"Between the two stacks is the logic to perform serial to parallel and parallel to serial conversion and generate the stack control signals so that one stack performs a push operation and the other performs a pop operation." (Paul Rendell, 2011)
"The other item visible is the delay loop for the next state which extends from the centre towards the left top corner underneath the left stack. The next state value is copied from the data read from the finite state machine and sent round this loop to address the finite state machine for the next cycle in conjunction with the symbol popped from one of the stacks." (Paul Rendell, 2011)
Rule 110 Cellular Automaton
The Rule 110 cellular automaton (often simply Rule 110) is an elementary cellular automaton with interesting behavior on the boundary between stability and chaos. In this respect it is similar to Conway's Game of Life. Also like Life, Rule 110 is known to be Turing complete. This implies that, in principle, any calculation or computer program can be simulated using this automaton.
A computational system that can compute every Turing-computable function is called Turing complete (or Turing powerful). Alternatively, such a system is one that can simulate a universal Turing machine.
In an elementary cellular automaton, a one-dimensional pattern of 0s and 1s evolves according to a simple set of rules. Whether a point in the pattern will be 0 or 1 in the new generation depends on its current value, as well as on those of its two neighbors. The Rule 110 automaton has the following set of rules:
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| new state for center cell | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
The name "Rule 110" derives from the fact that this rule can be summarized in the binary sequence 01101110; interpreted as a binary number, this corresponds to the decimal value 110.
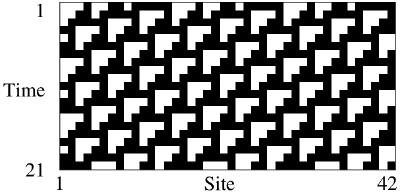
The implementation of Rule 110 is not complicated with the help of softwares. There’re already some good examples written in different languages. I took advantage of one written for Processing by Serdar Ormanli, in order to generate some images of Rule 110. Below is an example run of a rule 110 cellular automaton with 300 generations.
The function of the universal machine in Rule 110 requires an infinite number of localized patterns to be embedded within an infinitely repeating background pattern. The background pattern is fourteen cells wide and repeats itself exactly every seven iterations. The pattern is 00010011011111, shown as below.
If we filter away this background pattern, there are clearly some particle-like patterns left, which we can see in the below picture. These patterns move and collide according to consistent rules.
Three localized patterns are of particular importance in the Rule 110 universal machine. They are shown in the image below, surrounded by the repeating background pattern.
"The leftmost structure shifts to the right two cells and repeats every three generations. It comprises the sequence 0001110111 surrounded by the background pattern given above, as well as two different evolutions of this sequence. In the figures, time elapses from top to bottom: the top line represents the initial state, and each following line the state at the next time.
The center structure shifts left eight cells and repeats every thirty generations. It comprises the sequence 1001111 surrounded by the background pattern given above, as well as twenty-nine different evolutions of this sequence.
The rightmost structure remains stationary and repeats every seven generations. It comprises the sequence 111 surrounded by the background pattern given above, as well as five different evolutions of this sequence." (Wikipedia, Rule 110)
Reference
Stephen Wolfram, A New Kind of Science
Carl S. McTague, James P. Crutchfield, Automated pattern detection: An algorithm for constructing optimally synchronizing multi-regular language filters
Paul Rendell, A Universal Turing Machine in Conway’s Game of Life
Paul Rendell, Turing machine universality of the game of life
http://golly.sourceforge.net
http://conwaylife.com
http://www.binarydigits10.com/articles/conwaysgameoflife
http://rendell-attic.org/gol/utm/
https://github.com/ormanli/Rule-110
https://en.wikipedia.org/wiki/Rule_110